Fueling sense making.
This is the point of being a teacher in any subject, right? Finding ways to push students from being mere recipients of information to thinking critically about that information and using it to construct their own real knowledge.
For years I have battled within myself about the merits of memorizing math facts. I know being fast at math is not an indication of being “good” at math, but recalling basic math facts quickly sure does leave more energy for the problem solving aspect. I also know having math facts memorized doesn’t necessarily mean you totally get the concept of the four basic operations. I have seen this begin to cause problems in middle school as working with such concepts as fractions, ratios, and proportions require more than just good multiplication and division fact recall.
True sense-making requires the development of fluency, the ability to think flexibly {adjusting strategies} and critically {making connections to other concepts} while producing answers efficiently. But what role do I, as the teacher, play in fluency development?
There are a couple of learning theories illustrated in the coursework for Module 4 that help me address this question for myself. The first one considers the stages of mastery and the second illustrates the idea of concreteness fading.
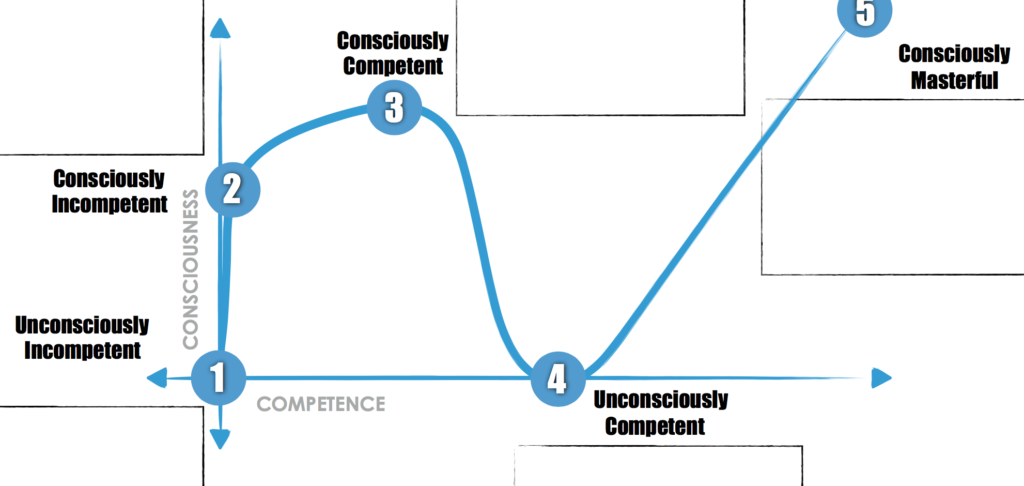
I have often looked at a student’s work, considered his thinking, and commented that he arrived at the correct answer, but doesn’t really understand the concept. What I never really thought about before is exactly where this student is on the mastery continuum and how I can push him to the next stage. The goal is to take students from being Unconsciously Incompetent to Consciously Masterful.
Credit: Kyle Pearce and Jon Orr, Making Math Moments That Matter
This visual representation of the stages of mastery was somewhat of an aha moment for me. Describing the steps along the journey in terms of consciousness and competence makes sense when I think about interactions I have had with students over the years. When a student responds to a question with an idea that clearly indicates he has no understanding of the concepts, he doesn’t know what he doesn’t know and is unconsciously incompetent. As he is introduced to a few ideas about the topic, he begins to understand that he knows what he doesn’t know to be successful. He is consciously incompetent. A student who is consciously competent is successful but it takes a good amount of time and energy to think it through and arrive at a correct solution. With some experience, he may become unconsciously competent, meaning he doesn’t have to put a lot of thought into a solution or answer because he just knows.
When this continuum was illustrated with a basic multiplication fact as an example, I was surprised a bit by what it looks like at each stage. It never really occurred to me that students in different stages of multiplication mastery could use the same strategies, but for different reasons. For example, a student who is unconsciously incompetent when thinking about multiplication will use one-to-one counting when presented with an array of objects. He will do this because he doesn’t have any idea there is a more efficient way. Another student, who is consciously incompetent, may attempt to use a different strategy for the same task but may settle on one-to-one counting because he can’t really figure out how to make another strategy work. The image on the left represents unconsciously incompetent, while the image on the right represents consciously incompetent.
Credit: Kyle Pearce and Jon Orr, Making Math Moments That Matter.
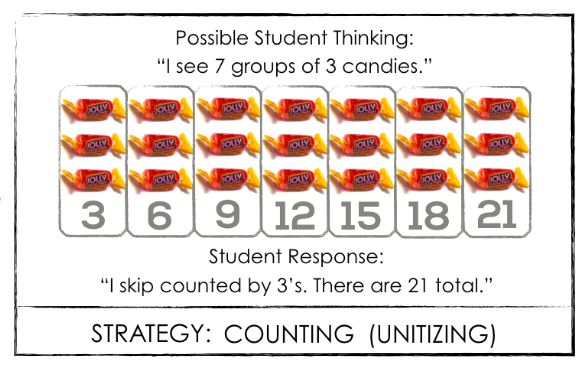
In this multiplication example, a student who is consciously competent (left image below) may begin to skip count. He sees groups of three candies and counts by threes to 21. A student who is unconsciously competent (right image below) will look at this same array and just “know” there are 21.
Credit: Kyle Pearce and Jon Orr, Making Math Moments That Matter.
Further, most of us might think that being unconsciously competent is the end goal. There is, in reality, a stage of mastery that is beyond this. A student who is consciously masterful not only demonstrates understanding of a concept, but is flexible in his thinking and can apply adapt strategies to fit a situation, providing multiple representations. For the stages of multiplication, it might look something like this:

Credit: Kyle Pearce and Jon Orr, Making Math Moments That Matter.
Some folks might wonder why this kind of thinking is important. Isn’t it enough to know 3 x 7 = 21? Well, sometimes it is enough. In other situations, especially as students move up through the ranks and encounter increasingly complex problems, flexibility in thinking and applying what they know in new ways becomes a necessity.
Enter the Concreteness Fading Model.
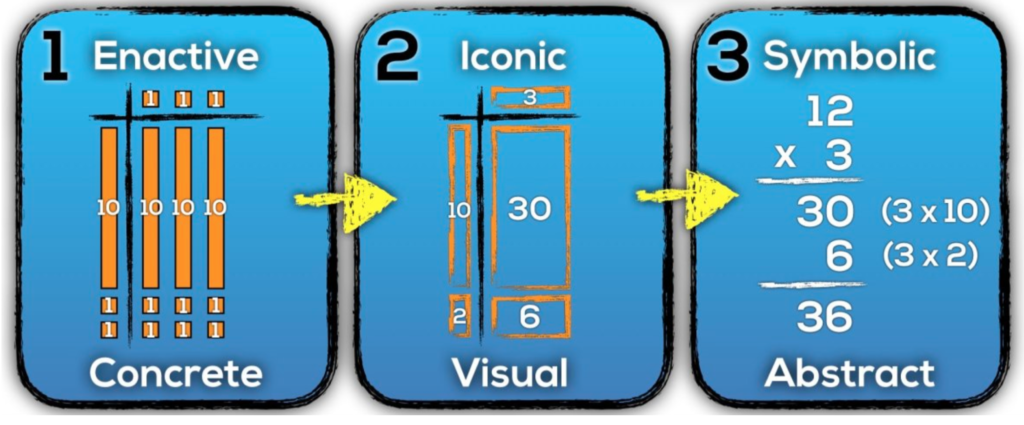
Basically, this model is the same as what I was trained to use as an elementary teacher. Begin with something concrete, like the actual candies. Next, move into some visual representation, like drawing shapes to represent candies or using base 10 blocks to represent numbers of candies. Finally, shift from visuals to what it looks like using expressions and equations with math symbols.
What struck me as different about Kyle and Jon’s take on this process is how they extended the idea of concreteness fading in multiplication all the way to what we traditionally think of as Algebra. {I am sure it can go even further, but algebra class is where they chose to end the progression.}
In the enactive, or concrete, stage of the model, base 10 blocks became the go to for representing larger numbers in a concrete way. Here, they are decomposed into 100s, 10s, and 1s and placed in an array. The iconic, or visual, stage of the model uses area model drawings to represent numbers in different ways than base 10 blocks may allow. These stages make way for the final symbolic, or abstract, stage where drawings are replaced with “standard” mathematical symbols.
Credit: Kyle Pearce and Jon Orr, Making Math Moments That Matter
The presentation of multiplication in this way really makes me want to reteach multiplication to ALL my middle grades students. Many of them never learned math facts well enough to be in the consciously competent stage of mastery. Many of them are still using one-to-one counting strategies to determine how many objects are in an array and several others are using skip counting or counting on from a known product to multiply. My eighth grade students are having difficulty learning how to use exponents and scientific notation. Most of my seventh grade students still struggle with proportional reasoning and percentages, even after months of practice. My sixth grade students have trouble with area and finding equivalent ratios. I believe all of these difficulties stem from a lack of true understanding of multiplication. These students are still in the early stages of mastery and have never been pushed to be unconsciously competent or consciously masterful in this important concept.
In the future, I need to be really mindful of where students are on the mastery continuum and find ways to push them forward in their thinking so they can not only be competent in math, but demonstrate the reflective and flexible thinking necessary to be fluent mathematicians.
What stages of mastery are your students exhibiting and what moves are you making to encourage sense-making and fluency?